P และ NP คืออะไร

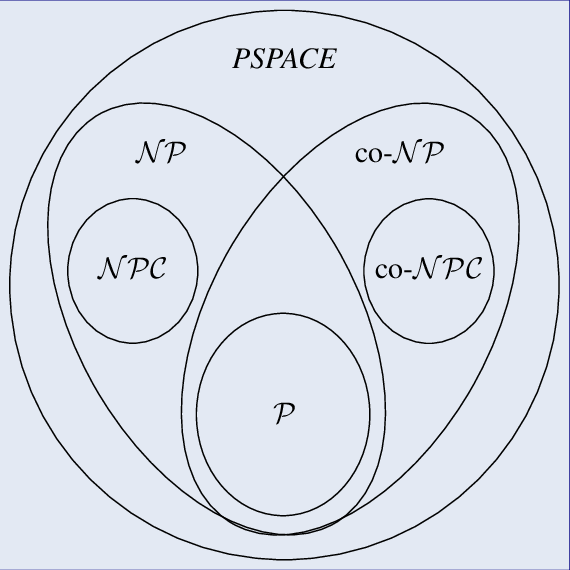
P = NP หรือไม่ เป็นหนึ่งในปัญหาทางคณิตศาสตร์ที่ยังไม่สามารถหาคำตอบได้ และถือเป็นหนึ่งในปัญหาที่โด่งดังในแวดวงคณิตศาสตร์และคอมพิวเตอร์ ผมเชื่อว่าหลาย ๆ คนที่เรียนเกี่ยวกับสายคณิตศาสตร์หรือคอมพิวเตอร์อาจจะได้เคยยินคุ้นหูกันมาบ้าง และอาจจะสงสัยว่า สรุปแล้ว P และ NP คืออะไรกันแน่ วันนี้ผมจึงจะมาอธิบายเกี่ยวกับความหมายของ P และ NP ซึ่งกลุ่มปัญหา P และ NP ก็สามารถนิยามได้ดังต่อไปนี้ 

มาถึงตรงนี้ก็มีศัพท์เฉพาะเยอะแยะไปหมด หลายคนอาจจะสงสัยว่าปัญหาตัดสินใจคืออะไร? Polynomial time คืออะไร ? สัญลักษณ์ O()  คืออะไร? ผมจึงจะขออธิบายความหมายของศัพท์เหล่านี้ก่อน 

ปัญหาการตัดสินใจ

ปัญหาการตัดสินใจ คือปัญหาที่มีคำตอบแค่หนึ่งในสองค่า เช่น ได้/ไม่ได้, ใช่/ไม่ใช่, มี/ไม่มี ซึ่งปัญหาที่ไม่ใช่ปัญหาการตัดสินใจก็สามารถแปลงเป็นปัญหาการตัดสินใจได้ เช่น ปัญหา 0/1knapsack  ที่เลือกหยิบของที่มีมูลค่าและพื้นที่ที่ต่างกันลงในกระเป๋าที่มีความจุจำกัดให้ได้มูลค่ารวมมากที่สุด ก็สามารถเปลี่ยนเป็นจะสามารถเลือกหยิบของให้รวมกันมีมูลค่าไม่ต่ำกว่า k แทนได้หรือไม่ เป็นต้น 

สัญลักษณ์ O() หรือที่เราเรียกกันว่า big O มีความหมายทางการเขียนโปรแกรมคือ เวลาที่ใช้ในการทำงานของโปรแกรมในกรณีที่ เลวร้ายที่สุด เท่าที่จะเป็นไปได้ โดยมี n คือจำนวนข้อมูลที่รับเข้ามา เช่น หากเรามีตัวเลขอยู่แถวหนึ่งจำนวน 10 ตัวเลข และต้องการเรียงตัวเลขจากน้อยไปมาก  คิดแบบง่าย ๆ ก็คือเราก็จะต้องทำการวนซ้ำหาเลขที่น้อยที่สุดในแต่ละครั้ง และหยิบออกมาวางไว้ในอีกแถวหนึ่ง

ทำแบบนี้เรื่อย ๆ จนกว่าจะไม่เหลือตัวเลขในแถวเก่าทั้งหมด (ที่จริงแล้ววิธีนี้เป็นวิธีที่แย่ จะมีวิธีที่เร็วกว่านี้มากมาย เช่น quick sort หรือ bucketing sort เป็นต้น แต่เพื่อให้เข้าใจง่าย ๆ จึงขอยกตัวอย่างวิธีที่คิดตามได้ง่ายที่สุด) จะได้ว่าเราทำงานมากที่สุดจำนวน 10² ครั้ง ซึ่ง 10 เป็นจำนวนข้อมูลที่รับเข้ามา เพราะฉะนั้น จากโจทย์เดียวกันนี้ หากเรานำข้อมูลอื่นที่อาจจะมีจำนวนมากกว่าหรือน้อยกว่าข้อมูลชุดเดิม ก็จะได้ว่าโปรแกรมจะต้องทำงานจำนวนทั้งหมด O(n²) ครั้งนั่นเอง

Polynomial time complexity

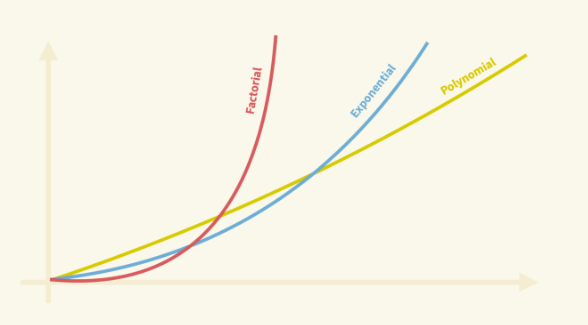
Polynomial time complexity คือเวลาที่ใช้ในการทำงานของโปรแกรมอยู่ในช่วง O(n^k) โดยที่ k เป็นจำนวนบวกและ k > 0 ซึ่ง Polynomial time ในการเขียนโปรแกรมนั้นถือว่าเป็นการทำงานที่เร็ว เมื่อเทียบกับ exponential time ที่มีเวลาในการทำงานของโปรแกรมอยู่ในช่วง O(kⁿ)

กราฟแสดงเวลาที่ใช้ใน time complexity แบบต่าง ๆ 

กลับมาที่กลุ่มปัญหา P และ NP ของเรากัน กลุ่มปัญหา P นั้นเข้าใจง่าย ๆ ว่าหาคำตอบได้โดยใช้เวลาเป็น Polynomial เช่นปัญหา 0/1Knapsack แบบแปลงเป็นปัญหาตัดสินใจแล้วอย่างที่ได้กล่าวไป เราสามารถใช้วิธีการวาดตารางขึ้นมา 1 ตาราง โดยให้แนวนอนเป็นน้ำหนักของของที่ใส่ในกระเป๋า และแนวตั้งเป็นของที่ใส่ในกระเป๋า และในแต่ละตาราง 

หากของที่จะใส่มีน้ำหนักไม่เกินกว่าแกนแนวตั้ง ให้พิจารณาว่าระหว่างมูลค่าของของที่จะใส่รวมกับแถวด้านบนและย้อนกลับไปจำนวนช่องเท่ากับน้ำหนักของของที่จะใส่ว่ามีมูลค่ารวมกันมากกว่าแถวด้านบนหรือไม่หรือไม่ ถ้ามากกว่าให้ใส่ ทำแบบนี้ไปเรื่อย ๆ หากเจอช่องใดที่มีน้ำหนักอย่างน้อย k ก็จะได้คำตอบว่ามี แต่ถ้าหาจนจบตารางแล้วยังไม่มีช่องใดมีค่าอย่างน้อย k ก็จะตอบว่าไม่มี จะได้ว่าเราใช้เวลาเป็น O(nw) โดยที่ n คือจำนวนสิ่งของที่พิจารณา และ w คือน้ำหนักของของที่รับได้ ซึ่งเวลาที่ใช้ยังอยู่ในปริภูมิของ Polynomial จึงถือว่าปัญหานี้เป็นกลุ่มปัญหา P 

ส่วนกลุ่มปัญหา NP นั้นจะเป็นการตรวจคำตอบแทนการหาคำตอบ คือเราได้รับคำตอบจากที่ไหนสักแห่งมาแล้วตรวจคำตอบโดยใช้เวลาไม่เกิน Polynomial time เช่น ปัญหา 0/1 Knapsack เราได้คำตอบมาเป็นแถวของข้อมูลที่มีจำนวนเท่ากับสิ่งของ โดยในแถวบรรจุเลข 0 หรือ 1 ไว้ หมายความว่าหากเป็น 0 คือไม่หยิบสิ่งนั้นเข้ากระเป๋า และ 1 คือหยิบสิ่งนั้นเข้ากระเป๋า ก็จะได้วิธีง่าย ๆ ว่าเลือกเฉพาะสิ่งของที่มีคำตอบเป็น 1

และนำของสิ่งนั้นมาบวกมูลค่าและน้ำหนักกัน หากมีมูลค่าอย่างน้อย k และมีน้ำหนักไม่เกินความจุกระเป๋าก็ถือว่าคำตอบนั้นถูกต้อง หรือเป็น yes นั่นเอง โดยวิธีการนี้ใช้เวลาอย่างมาก O(n) เท่านั้นเอง ซึ่งถือว่าอยู่ในปริภูมิเวลาของ Polynomial จึงถือว่าปัญหา 0/1Knapsack เป็นทั้ง P และ NP นั่นเอง 

ตัวอย่างอัลกอริทึมการตรวจคำตอบ 01 Knapsack

เขียนโดย เธียรวิชญ์ สิริสาครสกุล 

วันที่ 29 กรกฎาคม 2564 

อ้างอิง

• https://www.youtube.com/watch?v=sAXvv8LvIug&list=PL0ROnaCzUGB65_YkASLAEmcW_mtxFtq4m&index=77
• https://www.researchgate.net/figure/N-P-versus-co-N-P-Conjecture_fig14_267856474
• https://www.cantorsparadise.com/p-vs-np-what-is-the-difference-between-solving-a-problem-and-recognizing-its-solution-921c4c0df561